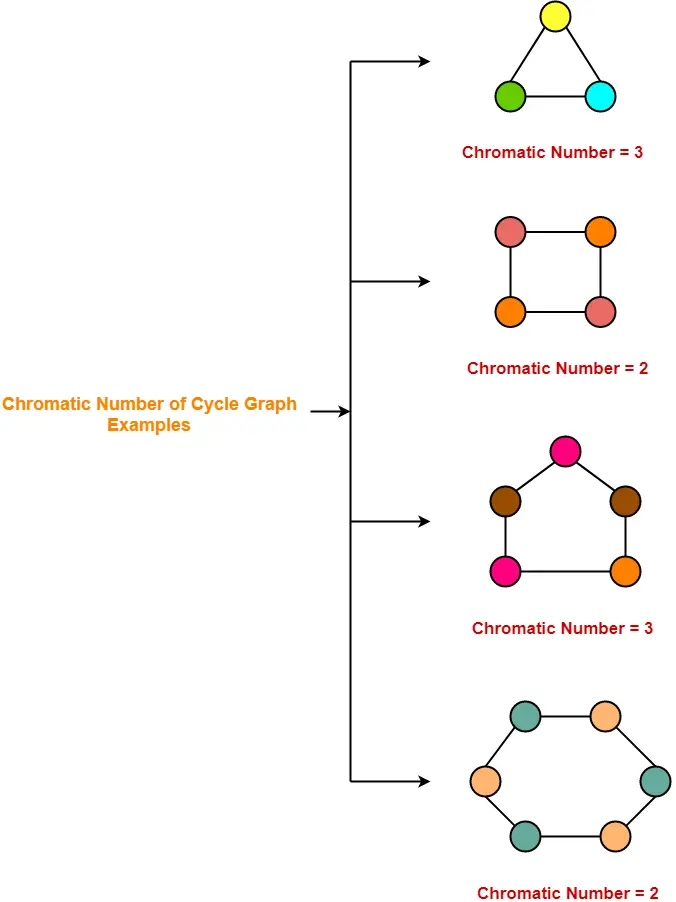
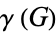Chromatic Number In Graph Coloring

Chromatic Number In Graph Coloring. The other graph coloring problems like Edge Coloring (No vertex is incident to two edges of same color) and Face Coloring (Geographical Map Coloring) can be transformed into vertex coloring. Graph Coloring is a process of assigning colors to the vertices of a graph.

Chromatic Number: graph coloring, graph theory | Glogster ... (Bill Waters)

Graph coloring problems model a collection of scheduling Given an n-vertex k-colorable graph, how many colors do you need in order to color the graph in polynomial time? Hint: Assign colors to vertices in order of non-increasing degrees such that no conflict arises. While graph coloring, the constraints that are set on the graph are colors, order of coloring, the way of assigning Simply put, no two vertices of an edge should be of the same color.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints.

In graph theory, graph coloring is a special case of graph labeling ; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain So this is a graph coloring problem where minimum number of time slots is equal to the chromatic number of the graph.

k-Chromatic Graph -- from Wolfram MathWorld

Chromatic Number -- from Wolfram MathWorld

Graph coloring

(PDF) On b-chromatic number of Sun let graph and wheel ...

Math for seven-year-olds: graph coloring, chromatic ...

How to Find Chromatic Number | Graph Coloring Algorithm ...

Graph Coloring in Graph Theory | Chromatic Number of ...

combinatorics - Planar graph with a chromatic number of 4 ...

chrompln

In this video, I explain what a coloring of a graph is in graph theory. Answer: c Explanation: Chromatic number of an arbitrary graph cannot be determined by using any convenient method. I also define the chromatic number of a graph and discuss a good procedure for.