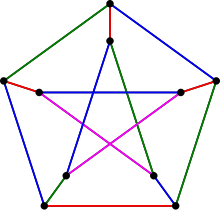
Chromatic Number In Edge Coloring

Chromatic Number In Edge Coloring. Since everything else in this file is derived from all_graph_colorings, this is a pretty good randomized tester for the entire file. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green.

Online Coloring Pages Tags : Coloring Book Online 42 ... (Beatrice Parks)

The (edge) chromatic number (χ′(G)) χ(G) of G is the minimum number of colors permitted in a such coloring. Some variants of vertex and edge coloring have been considered. The strong parity edge chromatic number p'(G) of G is the least k so that there is a coloring of E(G) using k colors with the property that every parity walk is closed.

Finding the chromatic number or chromatic polynomial for arbitrary graphs are computationally NP-hard problems.

JixiPix takes vintage to a whole new extreme. ¶ The chromatic number of a graph tells us about coloring vertices, but we could also ask about coloring edges.

Petersen graph - Wikipedia

Item Number Color Size (Nominal) Finish Application Look ...

Selected topics in finite mathematics/Graph coloring ...

Graph Coloring : Greedy Algorithm & Welsh Powell Algorithm

Outerplanar graph - Wikipedia

Crayola Art With Edge; Vanishing Numbers; Inspiration Art ...

Distinguishing coloring - Wikipedia

Online Coloring Pages Tags : Coloring Book Online 42 ...

TÓTH Ágnes

The chromatic number of G, denoted by X(G), is the smallest number k for which is k-colorable. Answer: a Explanation: The condition for proper coloring of graph is that two vertices which share a common edge should not have the same color. Number Of Colours Needed For A Proper Edge-colouring Of G (so That Edges With A Common Vertex Are Coloured Differently).