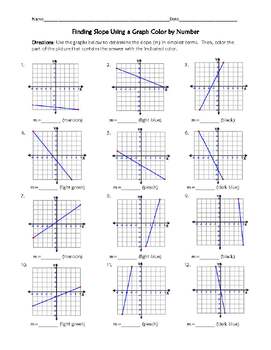
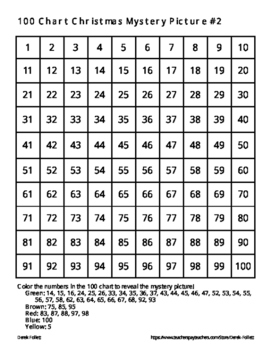
Coloring Number Of A Graph

Coloring Number Of A Graph. Given a graph $G$ it is easy to find a proper coloring: give every vertex a different color. Chromatic Number is the minimum number of colors required to properly color any graph.

FREE Printable Charts and Posters for Preschool and ... (Harriett Green)

The applet below provides a dynamic environment for coloring the nodes (vertices) of a graph. For example, only three colors are required for this graph colouring numbers for graphs excluding a xed minor, from the exponential bounds of. Inverting this relation, we have $$\chi But the USA graph is of a very special type.

Graph Coloring is a process of assigning colors to the vertices of a graph.

Inverting this relation, we have $$\chi But the USA graph is of a very special type.

1000+ images about 100 Chart on Pinterest | Hundreds chart ...

Vertex coloring · Martin Thoma

Fun graph art color-by-number pictures. See the picture ...

Finding Slope Using a Graph Color by Number by ...

Candy Hearts Graph | Graphing activities, Valentine ...

Graphing Systems of Inequalities Color by Number | Fun ...

Printable Fun Coordinate Graph Worksheets | Graphing ...

Preschool Color Chart | Preschool charts

Math: One Hundred 100 Chart Christmas Mystery Pictures ...

Grohe et al. to a linear bound for the r-colouring number colr Some generalisations of the colouring number of a graph have been studied in the literature. Chromatic Number is the minimum number of colors required to properly color any graph. In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject Coloring here means attaching a "color" or a number to each vertice such that no two vertices with a connecting edge have the save value..